En el caso de un brote de una nueva enfermedad, cuando no se dispone de una vacuna, el aislamiento de los infecciosos diagnosticados y la cuarentena de las personas son las únicas medidas de control disponibles.
Andrés Felipe Burgos Quintero
Estudiante de matemáticas de la Universidad de los Andes
José Ricardo Arteaga Bejarano
Profesor del Departamento de Matemáticas de la Universidad de los Andes
Por otro lado, para una ciudad como Bogotá, la movilidad de los individuos entre las diferentes localidades hace necesario un estudio metapoblacional en el que las medidas de control se puedan implementar separadamente. Consideramos dos zonas: la zona 1 (o zona norte) y la zona 2 (zona sur), las cuales son la unión de las poblaciones según su distribución geográfica. Al mismo tiempo, consideramos dos tipos de medidas de control. El primero consiste en acatar las medidas establecidas por la Alcaldía, como son el uso de tapabocas, el lavado frecuente de manos y el distanciamiento físico. El segundo tipo de medidas de control fue la movilidad de los individuos entre las dos zonas. El presente trabajo es un ejercicio únicamente de divulgación que muestra cómo las matemáticas ayudan a entender la dinámica del brote de una enfermedad, incluyendo factores importantes como las medidas de control. Ponemos énfasis en que los resultados y simulaciones son un simple juego y, por ningún motivo, no deben tomarse como predicciones, ni mucho menos, para hacer inferencias.
1. Introducción
El 30 de enero del 2020, la epidemia de la enfermedad coronavirus 2019 (covid-19) fue declarada una emergencia de salud pública a escala mundial por la Organización Mundial de la Salud (oms). El 6 de marzo del mismo año, el Ministerio de Salud y Protección Social en Colombia confirmó el primer caso de covid-19 en el territorio nacional.
El modelo Susceptibles, Infectados y Recuperados o Removidos (sir) es un modelo matemático propuesto en 1927 por William Ogilvy Kermack y Anderson Gray McKendrick, también conocido como modelo de Kermack-McKendrick. Está basado en el modelo de transmisión de la malaria de Ross-MacDonald.
El sir es un modelo compartimental en el que las tasas de transferencias entre compartimientos son expresadas como derivadas con respecto al tiempo, y su formulación es un sistema dinámico de tres ecuaciones diferenciales. Los supuestos de este modelo son: ley de acción de masas, la tasa a la cual una enfermedad se propaga es proporcional al número de individuos susceptibles por el número de individuos infecciosos; tasa de salida de los enfermos, los infectados dejan esta clase a una tasa proporcional al número de individuos infectados. Además, se supone que la población permanece constante y que se adquiere inmunidad permanente en caso de haber sido infectado.
Existen muchas enfermedades infectocontagiosas que se pueden modelar con el sir, por ejemplo, una epidemia de influenza. Sin embargo, para otras enfermedades no es recomendable utilizar este modelo, puesto que no satisfacen los supuestos. Por ejemplo, la gonorrea no satisface el supuesto de inmunidad permanente.
[1] Sir Ronald Ross md, fue Premio Nobel en Medicina en 1902 por su demostración de las dinámicas de transmisión de la malaria entre mosquitos y humanos y George MacDonald.
2. Métodos
Comenzaremos estableciendo un modelo teórico basado en trabajos de Fang et al. [4] y Avecillas et al. [5], quienes estudiaron casos similares en algunas provincias de China y Nueva York, respectivamente. No hemos hecho ajuste de los parámetros del modelo a los datos y por tanto usaremos valores encontrados en la literatura. Con estos parámetros, y jugando un poco con los parámetros de control que definiremos más adelante, mostraremos varias simulaciones.
2.1. Modelo matemático
Formulamos un modelo basado en dos modelos para describir el curso de una epidemia. El primero introducido por Gumel et al. [9] para modelar la epidemia de sars de 2002-2003 en Toronto, y un segundo, formulado por Avecillas et al. [5], quien consideró metapoblaciones para el estudio de las dinámicas del covid-19 en Nueva York. Basados en este par de modelos matemáticos formulamos un modelo matemático teórico, adaptado a Bogotá, con el cual se busca entender, desde el punto de vista matemático, la dinámica del covid-19 cuando se implementen las medidas de control. Ni el modelo formulado ni las simulaciones deben tomarse como resultados para hacer predicciones ni mucho menos para hacer inferencias. Además, es una primera aproximación de un trabajo que quisiéramos continuar estudiando.
El modelo que usaremos para entender mejor las dinámicas del COVID-19 en la ciudad de Bogotá es un modelo metapoblacional con dos poblaciones correspondientes a la zona norte (i=1) y a la zona sur (i=2) de la ciudad, el cual denotaremos por como SEAIR. Para cada una de las metapoblaciones las clases susceptibles (Si) están compuestas por individuos que no han sido expuestos a la enfermedad. Hay un periodo de latencia o exposición (Ei) después del la cual una fracción (σ) de los individuos latentes (Ei) pasa a un estadio infeccioso asintomático: 
con infectividad reducida por un factor δ, mientras que la fracción restante (1 - σ) pasa a un estadio infeccioso sintomático: La clase de infecciosos, por lo tanto, está compuesta por la unión de asintomáticos y sintomáticos. La tasa que de los individuos expuestos que se convierten en infectados es : 
donde q es el periodo de incubación. Definimos μ como la tasa de letalidad causada por la enfermedad. Cabe resaltar que esta tasa es casi nula en pacientes asintomáticos según las fuentes consultadas, quizá por desconocimiento si se padecía de la enfermedad o por no estar reportados en entidades de salud. Por tal motivo, solo se tendrá en cuenta para pacientes sintomáticos.
Por último, si se considera a c como el periodo de recuperación de la enfermedad, entonces la constante 
corresponde a la tasa de recuperación. Además de los seis parámetros del modelo enunciados anteriormente agregaremos los siguientes parámetros de control:un parámetro escalar
∈ [0,1] para cada metapoblación y un parámetro matricial Pij ∈ [0,1] de acoplamiento de las dos metapoblaciones. El primer parámetro
representa el posible impacto que tienen las medidas de control dentro del modelo como son el uso de tapabocas, el distanciamiento de mínimo 2 metros entre cada persona, el lavado frecuente de manos, entre otras. Es decir, si
= 0 significa que en la zona i no se práctica ninguna medida control. Mientras que si ai = 1, significa que se toman en cuenta todos los protocolos y, por consiguiente, no hay posibilidad de nuevas infecciones en dicha zona en el caso de que no haya contactos con individuos de la otra zona. El segundo parámetro matricial pij captura adecuadamente la dinámica de la enfermedad de contactos entre las dos metapoblaciones al definirendo la proporción de tiempo que un individuo residente de la zona i permanece en la zona j. Por ejemplo, si p11 = 1 signfica que los individuos de la zona uno solo tienen contactos directos con individuos de su propia zona y, por lo tanto, p12 = 0. Es decir, Σ j2 =1 p11 =1. El modelo a estudiar es,
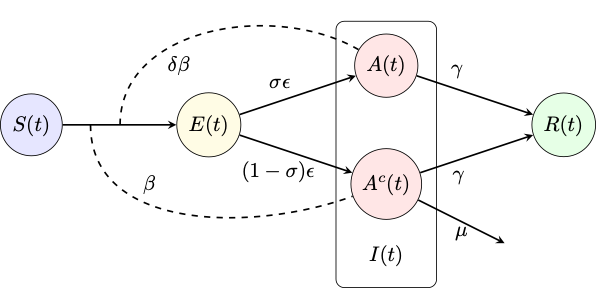
Diagrama de flujo del modelo SEAIR para cada metapoblación, donde I (t)=A(t) ∪ Ac(t)
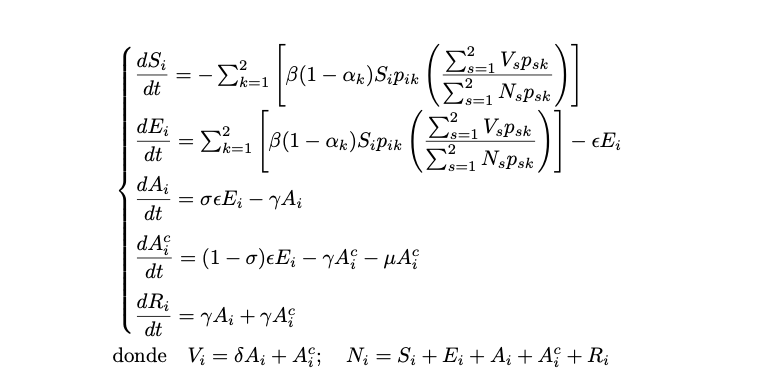
2.2. El número reproductivo básico (R0)
La idea fundamental del número reproductivo básico (R0) es si pensamos en introducir una pequeña cantidad de infecciosos en una población de susceptibles y nos preguntamos si habrá una epidemia. La cantidad R0 es una cantidad umbral que da respuesta a esta pregunta. Si R0 <1 la infección se extingue, mientras que si R0 >1, hay una epidemia. La definición del número de reproducción básico (R0) es el número de infecciones secundarias causadas por un único infeccioso introducido en una población totalmente susceptible. Quizá el aporte más grande de las matemáticas en la Eepidemiología es este número, el cual se formalizó su cálculo para cualquier modelo compartimental de enfermedades infecciosas. La demostración se puede encontrar en los trabajos de Heesterbeek (1990, 1991) [10, 11]. En las simulaciones calculamos, para nuestro modelo, la Matriz de la Próxima Generación (NGM) y su radio espectral que es el número reproductivo básico (R0).
3. Resultados
Los resultados mostrados en las simulaciones se basan en datos confirmados por el Observatorio de Salud de Bogotá [7], el Ministerio de Salud y Protección Social de Colombia [3], y la oms (who) [2] para prevención de enfermedades y de la literatura.
3.1. Datos
La tabla 1, que está compuesta por zona 1 (norte) y zona 2 (sur), resume el nombre de la localidad de Bogotá, el tamaño de su población total, el número de individuos confirmados (la información tiene un desfase de dos semanas aproximadamente, debido a los resultados de la prueba rt-pcr para covid-19), el número de individuos recuperados y el número de individuos fallecidos. Los datos fueron tomados del Observatorio de Salud de Bogotá [7].
Tabla 1. Distribución de casos confirmados covid-19 (fecha de observación: 12 de octubre del 2020)
| Zona 1 (norte) | Población | Confirmados | Recuperados | Fallecidos |
| Usaquén |
476.184 | 16.660 |
15.331 |
380 |
Suba |
1.348.372 | 38.559 |
35.646 |
878 |
Engativá |
887.886 | 30.606 |
28.180 |
770 |
Barrios Unidos |
237.396 | 5.790 |
5.328 |
186 |
Chapinero |
125.750 | 6.287 |
5.789 |
167 |
Teusaquillo |
139.776 | 5.046 |
4.569 |
142 |
Fontibón |
434.446 | 13.031 |
12.010 |
298 |
Santa Fe |
92.490 | 5.011 |
4.589 |
157 |
La Candelaria |
22.041 | 1.250 |
1.135 |
35 |
Los Mártires |
92.755 | 3.950 | 3.613 |
116 |
| Totales zona 1 | 3.857.096 | 126.190 | 116.190 | 3.129 |
|
Zona 2 (sur) |
Población |
Confirmados |
Recuperados |
Fallecidos |
| Puente Aranda |
251.191 |
11.869 |
10.942 |
327 |
| Kennedy |
1.252.014 |
39.686 |
36.811 |
1.001 |
| Bosa |
776.363 |
25.635 |
23.846 |
581 |
| Antonio Nariño |
109.104 |
4.119 |
3.767 |
152 |
| Tunjuelito |
184.743 |
7.965 |
7.221 |
274 |
| Rafael Uribe Uribe |
344.990 |
15.143 |
13.972 |
421 |
| San Cristóbal |
389.945 |
14.900 |
13.728 |
431 |
| Ciudad Bolívar |
762.184 |
20.632 |
18.942 |
526 |
| Usme |
345.689 |
11.674 |
10.718 |
306 |
| Sumapaz | 7.711 |
2.747 |
2.515 |
96 |
Totales zona 2 |
4.423.934 | 154.370 | 142.462 | 4.115 |
En segundo lugar, para la conformación de los parámetros del modelo, la tabla 2 muestra la notación usada, su descripción, los valores usados para la simulación, sus unidades y la referencia correspondiente.
Tabla 2. Parámetros del modelo
| Parámetro | Descripción | Valor | Unidades | Referencia |
| β | Tasa de transmisión de la enfermedad | 0,185 | días-1 | [4] |
| δ | Factor de disminución de contagios con individuos asintomáticos | 30 % | N/A | [5] |
| ϵ | Tasa de transición de expuesto a infectado | 0,2 | días-1 | [6] |
| σ | Proporción de infectados que son asintomáticos | 37,3 % | N/A | [7] |
| γ | Tasa de recuperación | 0,071 | días-1 | [8] |
| μ | Tasa de letalidad por causa del covid-19 | 0,025 | días-1 | [7] |
Finalmente, la tabla 3 muestra los dos tipos de parámetros de control considerados en las simulaciones.
Tabla 3. Parámetros de control
| Parámetro | Descripción | Valor | Unidades |
 |
Proporción de individuos en la zona norte que siguen las precauciones recomendadas | [0,1] | N/A |
 |
Proporción de individuos en la zona sur que siguen las precauciones recomendadas | [0,1] | N/A |
 |
Proporción de tiempo que residentes de la zona i permanece en la zona j | [0,1] | N/A |
3.2 Simulación del modelo y discusión
En la figura 1 se muestra, a la izquierda la zona 1 y a la derecha la zona 2, el resultado de la siguiente simulación es: Las condiciones iniciales son: I1 (0)=6871, I2 (0)=7793 respectivamente, donde Ii (0)=Ai(0)+Aci (0). Es decir, el número total de infectados, sintomáticos y asintomáticos, correspondientes a cada zona. La línea punteada roja representa la dinámica sin acatamiento de las medidas de control tipo 1 (uso de tapabocas, distanciamiento de mínimo 2 metros entre cada persona, lavado frecuente de manos, y otras). Observe que al aumentar el porcentaje de acatamiento de las medidas de control tipo 1, se disminuye la prevalencia puntual de la enfermedad. Si la aceptación de estas medidas es mayor al 30 % de la población total, no hay epidemia independiente de las zonas (el número reproductivo básico R0<1).
El “pico” de la epidemia en la zona sur siempre es mayor que el “pico” de la zona norte debido su mayor tamaño poblacional. Respecto a las medidas de control tipo 2 (proporción de tiempo que los residentes de la zona i permanecen en la zona j ), que interpretamos como movilidad, están fijas con los siguientes valores: p11 =p12=0,85, p11 =p21 =0,15. Estos números presuponen que el 30 % de la población de una zona que se desplaza a la otra zona durante 12 horas en promedio. El número reproductivo básico R0 se calculó con el radio espectral de la matriz de la próxima generación. Los resultados numéricos de las simulaciones confirman lo conocido en la teoría, es decir, si R0>1 se nota una epidemia y, en caso contrario, no.
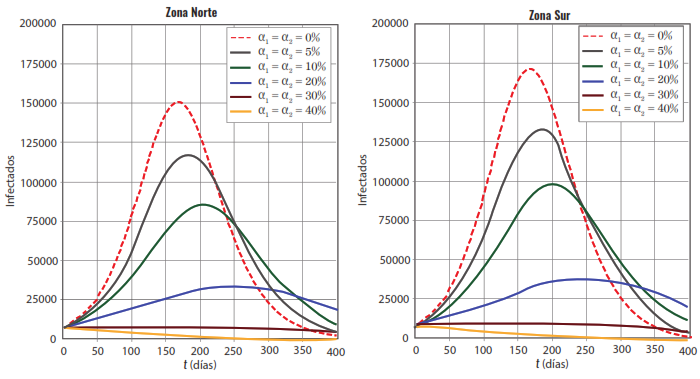
Figura 1. A la izquierda se muestran los resultados para la zona 1 y a la derecha para la zona 2.
El eje horizontal es el tiempo en días y el eje vertical es el número de individuos infectados correspondiente a cada zona. Las condiciones iniciales son: I1 (0)=6871, I2 (0) = 7793 respectivamente. La línea punteada roja representa la dinámica sin acatamiento de las medidas de control tipo 1 (tapabocas, etc.). Las demás líneas continuas representan la variación de la dinámica de la dispersión de la enfermedad cuando se aumenta el acatamiento de las medidas de control tipo 1. En la figura 2 se muestra, a la izquierda la zona 1 y a la derecha la zona 2, el resultado de otra simulación. Las condiciones iniciales son iguales a las de la simulación anterior junto con los valores para pij. En este caso, las medidas de control tipo 1 no se mantienen idénticas para ambas zonas. Observe que, si en una zona el nivel de acatamiento es, por ejemplo, del 40 % y en la otra del 0 %, ambas poblaciones desarrollan epidemia. Si se quiere que no haya epidemia, ambas poblaciones deberían cumplir el mismo nivel de acatamiento de las medidas de control tipo 1 de al menos el 30 % como lo muestra la figura 1.
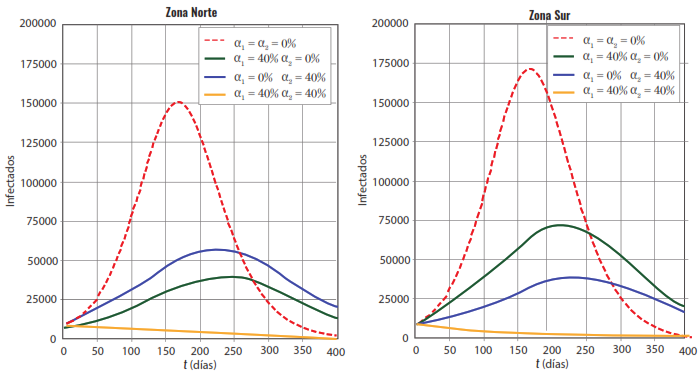
Figura 2. A la izquierda se muestran los resultados para la zona 1 y a la derecha para la zona 2.
El eje horizontal es el tiempo en días y el eje vertical es el número de individuos infectados correspondiente a cada zona. Las condiciones iniciales son: I1 (0) = 6871, I2 (0) = 7793 respectivamente. La línea punteada roja representa la dinámica sin acatamiento de las medidas de control tipo 1 (tapabocas, etc.). Las demás lineas continuas representan la variación de la dinámica de la dispersion de la enfermedad cuando el nivel de acatamiento de las medidas de control tipo 1 son es diferentes para las dos zonas.
Conclusión
El modelo presentado anteriormente, muestra más evidencias de que podemos utilizar este tipo de modelos matemáticos frente a brotes de enfermedades, cuando no se dispone de una vacuna y las únicas medidas de control plausibles son: la restricción a la movilidad (confinamiento obligatorio) y el autocuidado (acatamiento de las medidas de bioseguridad). Como conclusión, para que no haya epidemia en ninguna subpoblación de un sistema metaploblacional conectado, es necesario que se satisfagan las medidas de control de bioseguridad aproximadamente al mismo nivel. En el caso mostrado para dos subpoblaciones con las condiciones establecidas anteriormente, este nivel debe ser mayor al 30 %. No se mostraron simulaciones manteniendo fijas las medidas de autocuidado y variando la movilidad, debido a que los resultados no fueron significativos.
Referencias
[1] Brauer F, Castillo-Chávez C. Mathematical Models in Population Biology and Epidemiology. 2nd ed. New York: Springer; 2012.
[2] World Health Organization. Coronavirus disease 2019 (covid‐19) situation report (40). https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200229-sitrep-40-covid-19.pdf?sfvrsn=849d0665_2
[3] Ministerio de Salud y Protección Social. Colombia confirma su primer caso de covid-19. 2020. https://www.minsalud.gov.co/Paginas/Colombia-confirma-su-primer-caso-de-covid-19.aspx
[4] Manrique-Abril F, Agudelo-Calderón C, González-Chordá V, Gutiérrez-Lesmes O, Téllez-Piñerez C, Herrera-Amaya G. Modelo sir de la pandemia de covid-19 en Colombia. Rev. Salud Pública 2020, 22(2): 1-9. doi: 10.15446/rsap.v22n2.85977
[5] Avecillas G, Manns S, Tekle H, Rodríguez Rodríguez L, Yamamoto N. Analyzing the Control Measures for the Homeless Population and Quantifying their Impact on the covid-19 Epidemic in New York City, 7. 2020.
[6] Stephen A. Lauer, MS, PhD, Kyra H. Grantz, BA, Qifang Bi, MHS, Forrest K. Jones, MPH et al. The Incubation Period of Coronavirus Disease 2019 (covid-19) From Publicly Reported Confirmed Cases: Estimation and Application. Ann Intern Med. 2020 may. https://www.acpjournals.org/doi/10.7326/M20-0504
[7] Saludata. Casos confirmados de covid-19. 2020. http://saludata.saludcapital.gov.co/osb/index.php/datos-de-salud/enfermedades-trasmisibles/covid19/
[8] Gallagher J. ¿Cuánto tiempo lleva recuperarse del coronavirus? BBC News Mundo. 2020 ab. https://www.bbc.com/mundo/noticias-52338314
[9] Gumel A, Ruan S, Day T, Watmough J, Van den Driessche P, Brauer F, Gabrielson D, Bowman C, Alexander ME, Ardal S, Wu J, Sahai BM. Modeling strategies for controlling sars outbreaks based on Toronto, Hong Kong, Singapore and Beijing experience, Proc. Roy. Soc. London 2004; 271: 2223-2232.
[10] Diekmann O, Heesterbeek JAP, Metz JAJ. On the definition and the computation of the basic reproductive ratio R0 in models for infectious diseases in heterogeneous populations. J Math Biol 1990; 28: 365-382.
[11] Diekmann O, Dietz K, Heesterbeek JAP. The basic reproduction ratio for sexually transmitted diseases, Part 1: Theoretical considerations. Math Biosci 1991; 107: 325-339.
